题解：P2822 [NOIP2016 提高组] 组合数问题

思路

杨辉三角模板题。

想要深入了解杨辉三角可在百度百科中查看，这里仅稍作讲解。

我们知道组合公式：

\[C\textstyle\binom{n}{m}=\frac{n!}{m!(n-m)!}\]

而杨辉三角则是数形结合：

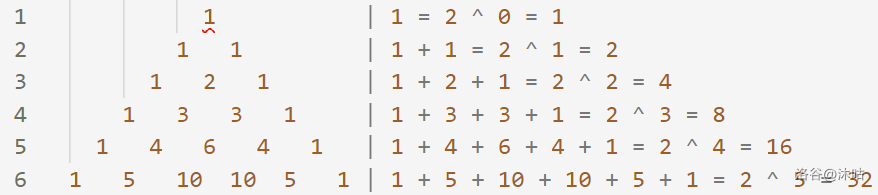
我们发现，$C(i, j)$ 为它左上角（$C(i - 1, j - 1)$）和右上角（$C(i - 1, j)$）的两个值的和。

当然也有一个在本题用不到的性质：第 $i$ 行的总和为 $2 ^ {i - 1}$。

这是我对于本题的思路推导：

第一步：计算杨辉三角。
第二步：计算杨辉三角对 $k$ 取模。
第三步：计算杨辉三角对 $k$ 取模后里面有几个 $0$。

为什么是对 $k$ 取模呢？

因为本题需要我们求有多少对 $(i, j)$ 满足 $k \mid C(i, j)$，因此我们对 $k$ 取模。

这样就基本没有问题了。

如果你想获得剩下的 $5$ 分，可以使用前缀和处理后面的大规模数据。

前缀和在本题主要有三个用途：

降低时间
例如，查询 $C(0, 0)$ 到 $C(5, 5)$ 的范围，需要遍历 $36$ 个（从 $(0, 0)$ 到 $(5, 5)$ 总共 $6 \times 6$ 个位置）组合数进行判断和计数。
而使用前缀和，我们只需要事先通过一次遍历计算，把所有可能的前缀和信息都存储在 $sum$ 数组中。后续查询任何一个范围时，直接通过 $sum_{x, y}$ 就能获取到对应的总和。
快速查询
假设我们想知道从 $C(a, b)$ 到 $C(n, m)$ 这个子区域内组合数取模为 $0$ 的个数总和，利用前缀和可以方便地通过几个简单的计算得出结果。
如果已经计算好了二维前缀和数组 $sum$，这个子区域的总和可以通过公式来得到。
这就相当于把整个二维区域的组合数按照一定顺序进行了所谓的“累加”存储在 $sum$ 数组中，通过简单的公式就能快速获取任意指定子区域的统计总和，而不需要再次去逐个查看子区域内的每个组合数情况。
契合本题
本题中程序的流程是先进行一些预处理（计算组合数取模和对应的前缀和），然后要根据输入的 $t$ 次不同的 $n$ 和 $m$ 值，去查询相应范围内组合数取模为 $0$ 的个数总和。
由于存在多次查询不同范围的情况，使用前缀和这种数据结构和计算方式，正好契合这种需求，能够在预处理阶段花费一定时间去计算前缀和，之后在多次查询阶段快速获取结果，能大大优化程序。

代码

#include<bits/stdc++.h>
using namespace std;
int c[2010][2010], sum[2010][2010];
void calcC(int n,int m,int k){
	memset(c,-1,sizeof(c));
	for(int i = 0;i <= n;i++){
		c[i][0] = c[i][i] = 1 % k;
		for(int j = 1;j < i;j++){ 
			c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
		}
	}
}
void calcSum(int n, int m) {
	for(int i = 0;i <= n;i++){
		sum[i][0] = (c[i][0] == 0);
		for(int j = 1;j <= m;j++){
			sum[i][j] = sum[i][j - 1] + (c[i][j] == 0);
		}
	}
	for(int i = 1;i <= n;i++){
		for (int j = 0;j <= m;j++){
			sum[i][j] = sum[i - 1][j] + sum[i][j];
		}
	}
	
}
int main(){
	int t,k,n,m;
	cin>>t>>k;
	calcC(2000,2000,k);
	calcSum(2000,2000);
	while(t--){
		cin>>n>>m;
		cout<<sum[n][m]<<endl;
	}
	return 0;
}